Introduction
Hello, I will try to explain in this post how I made my own TOTP(Time Based One Time Password) using c#
Many of us use authenticator apps like google authenticator
it basically generate a one time password every X seconds.
Then we can use this password to verify login or whatever.
Theory
I will explain the theory behind it in very simple words, Here is some math of how we will generate TOTP1
$$ \begin{align} TOTP(K) = HOTP(K, C_{T}) \bmod 10^d \\ \end{align} $$
where \(k\) is is the secret key shared between the server and the client.
and \(d \in \mathbb{N}\) represents number of digits in the password we need to generate.
The recommended range for d is 6 to 8 digits aims to strike a balance between security and user experience. The lower limit of 6 digits ensures a reasonable level of security, while the upper limit of 8 digits prevents excessive complexity and usability issues.
now to generate a value based on time we have a variable called \(C_{T}\)
$$ \begin{align} C_{T} = \lfloor \cfrac{T - T_{0}}{T_{x}} \rfloor \end{align} $$
Where:
\(C_{T}\) is the count of the number of durations \(T_{X}\) between \(T_{0}\) and \(T\)
\(T\) is the current time in seconds since a particular epoch
\(T_{0}\) is the epoch as specified in seconds since the Unix epoch (e.g. if using Unix time, then T0 is 0)
\(T_{X}\) is the length of one time duration (e.g. 30 seconds)
as explained in wikipedia article 1
to prove that it will generate same number in period \(T_{X}\) above take this example:
Let \(T_{0}\) be the initial time, \(T\) be the current time, and \(T_{X}\) be the time interval set to 30 seconds. If the difference between the current time \(T\) and the initial time \(T_{0}\) is within the same 30-second interval, the result of \(\lfloor \cfrac{T-T_{0}}{T_{X}} \rfloor\) will be the same, leading to the same value of \(C_{T}\)
For instance:
- If \(T\) is 0 seconds and \(T_{0}\) is \(0\) seconds, then \( \lfloor \cfrac{T-T_{0}}{T_{X}} \rfloor \) will be \( \lfloor \cfrac{0-0}{30} \rfloor = 0 \).
- If \(T\) is 15 seconds and \(T_{0}\) is \(0\) seconds, then \( \lfloor \cfrac{T-T_{0}}{T_{X}} \rfloor \) will be \( \lfloor \cfrac{15-0}{30} \rfloor = \lfloor 0.5 \rfloor = 0 \).
- If \(T\) is 30 seconds and \(T_{0}\) is \(0\) seconds, then \( \lfloor \cfrac{T-T_{0}}{T_{X}} \rfloor \) will be \( \lfloor \cfrac{30-0}{30} \rfloor = 1 \).
since \(T\) is number of seconds since epoch time, so \(T\) can be written as \(T = n \cdot T_{X} + y + T_{0}\) where \(n \in \mathbb{N} : n \mod T_{X} = 0 \) and \(0 \leq y \leq T_{X}\) so
$$ \begin{align} \left\lfloor \frac{T - T_0}{T_X} \right\rfloor \Rightarrow & \left\lfloor \frac{n \cdot T_X + y + T_{0} - T_0}{T_X} \right\rfloor \\ \Rightarrow & \left\lfloor \frac{n \cdot T_X}{T_X} + \frac{y}{T_X} \right\rfloor\\ &\Rightarrow \left\lfloor n + \frac{y}{T_X} \right\rfloor \\ \end{align} $$
and \(n \in \mathbb{N}\) so
$$ \begin{align} C_{T} = n + \lfloor \cfrac{y}{T_{x}} \rfloor \end{align} $$
we have \(0 \leq y \leq T_{X}\) so
$$ \begin{align} C_{T} = \begin{cases} n &\forall y \in [0,T_{X}[ \\ n+1 &\text{if } y = T_{X} \end{cases} \end{align} $$
so this is the proof that we will always get the same number in interval of \(T_{X}\)
for people with no mathmatical background ⌊x⌋ is nothing but floor(x)
after we covered the theory behind generating a number that doesn’t change in interval of time, we still have security concern, HOTP2 is a way to add security layer to the generated number, it generates a unique password based on shared secret key between two parties and \(C_{T}\) calculated.
I will not go through how to calculate HMAC mathmatically as it’s out of my interest and expertise.
I will explain what to do after generating HMAC hash, I am using HMAC512 which will generate a 64 byte array.
after we generate it we will take last 4 bits and use it as offset, the offset is nothing but adding more randomness into algorithm, maximum number we can get from 4 bits is 1111 which is 15 in decimal.So our offset will be 15 at maximum.
Then after that we will take starting from offset another 8 bytes (maximum number we can get from 8 bytes is 18446744073709551615)
but as we said the one time password is recommended to be between 6 and 8 so we will do mod operation to get first \(d\) digits.
Maybe it will be more clear when we write code for this one.
Coding
I know theory is boring for some people, but it’s essential to understand how algorithm works.
First I will start by writing the function that will calculate \(C_{T}\)
long CalculateCounter(long T0, long TX)
{
double T = (long)(DateTime.UtcNow - DateTime.UnixEpoch).TotalSeconds + T0;
long CT = (long)Math.Floor((T - T0) / TX);
return CT;
}
I am using UTC (universal time) because client may have different timezone than server so we need to use something that is universal.
\(T\) have total seconds that have passed since unix epoch time3
The code is nothing but implementation of \(C_{T}\) we explained in theory section.
1long GenerateHOTP(byte[] key, long counter, int digits = 6)
2{
3 using var hmac = new HMACSHA512(key);
4 byte[] counterBytes = BitConverter.GetBytes(counter);
5 if (BitConverter.IsLittleEndian) Array.Reverse(counterBytes);
6
7 byte[] hash = hmac.ComputeHash(counterBytes);
8
9 int offset = hash[hash.Length - 1] & 0x0F;
10
11 long nextEightBytesFromOffset = BitConverter.ToInt64(hash, offset) & 0x7FFFFFFFFFFFFFFFL;
12
13 return nextEightBytesFromOffset % (long)Math.Pow(10, digits);
14}
at line 3 I am using System.Security.Cryptography to create HMAC512 using a shared key.
HOTP is defined to use big-endian byte order for consistency across different platforms and systems. If your system is little-endian (like most modern computers), you need to reverse the byte order of the counter before using it in the HOTP calculation to ensure that it follows the required big-endian format. And that’s what I did at line 5
at line 9 I am calculating offset by getting last 4 bits. As I said before HMAC512 will generate a 64 bytes array and we interrested only in last 4 bits.
to get last 4 bits I am accessing last byte in hash, and because 1 byte is 8 bits I am doing a mask to eliminate first 4 most significant bits
To better visualize it let’s assume the last byte is 1100 0101 we need to mask it with 0x0F which have binary representation 0000 1111
1100 0101
&
0000 1111
------------
0000 0101
Like that we eliminated first 4 most significant bits
at line 11 BitConverter.ToInt64 will get the first 8 bytes from array so BitConverter.ToInt64(hash, offset) can be read like get get first 8 bytes from array hash starting from offset.
again I am using binary operation but this time to make sure that we are getting a positive number, MSB (Most significant bit) represent the sign of the number so by making it 0 we are making sure that the number generated is always positive.
binary representation of 0x7FFFFFFFFFFFFFFFL is nothing but one 0 followed by 63 ones.
then at line 13 I did the mod operation to get at most d digits.
now time to run application and see
static void Main()
{
Stopwatch sp = new();
sp.Start();
int intervalInSeconds = 30;
int T0 = 0;
int digits = 8;
for (int i = 0; i < 20; i++)
{
byte[] secretKey = Encoding.ASCII.GetBytes("i_am_secret_key");
long counter = CalculateCounter(T0, intervalInSeconds);
long hotpValue = GenerateHOTP(secretKey, counter, digits);
Console.WriteLine($"elapsed {sp.ElapsedMilliseconds / 1000} seconds");
Console.WriteLine($"HOTP value: {hotpValue:D8}");
Thread.Sleep(10000);
}
}
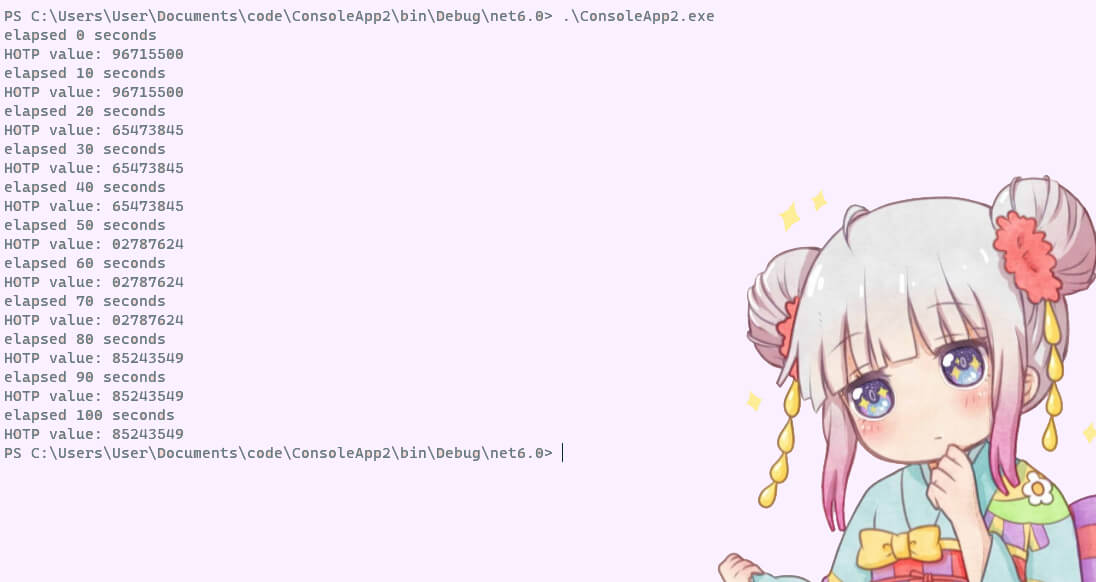
as we can see it’s generating new password in interval of 30 seconds. Now if server and client have same code used for generation and share same key, the server can calculate the one time password and check if it’s same as the one that client sents, if it is then you can login or do what ever step your app do after verifying user.
Storing secrets in code is bad practice and should be avoided, In real world setup it's better to store it in a vault, config file or environment.
Hope it was a good read and you learned new things.
To download source code click here
